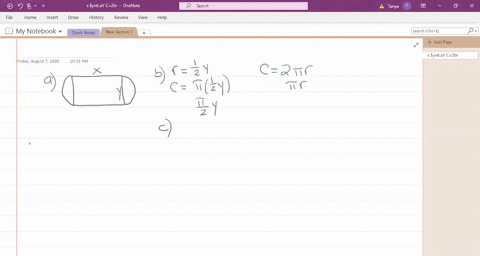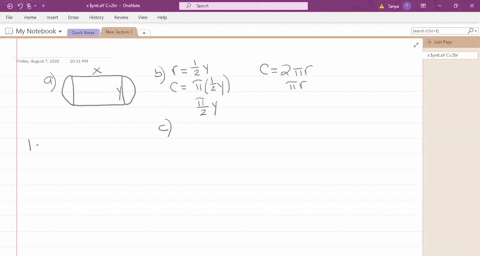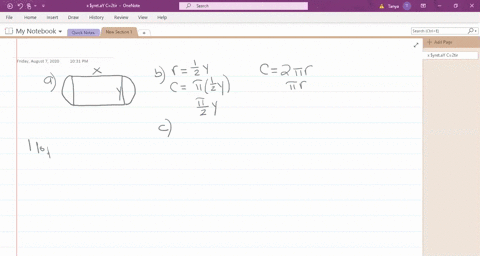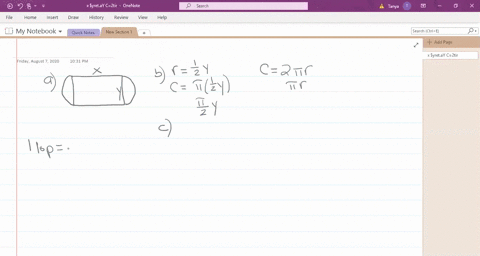
For the purpose of this problem the width will be the smaller dimension needing two sides. What dimensions produce a maximum enclosed area.
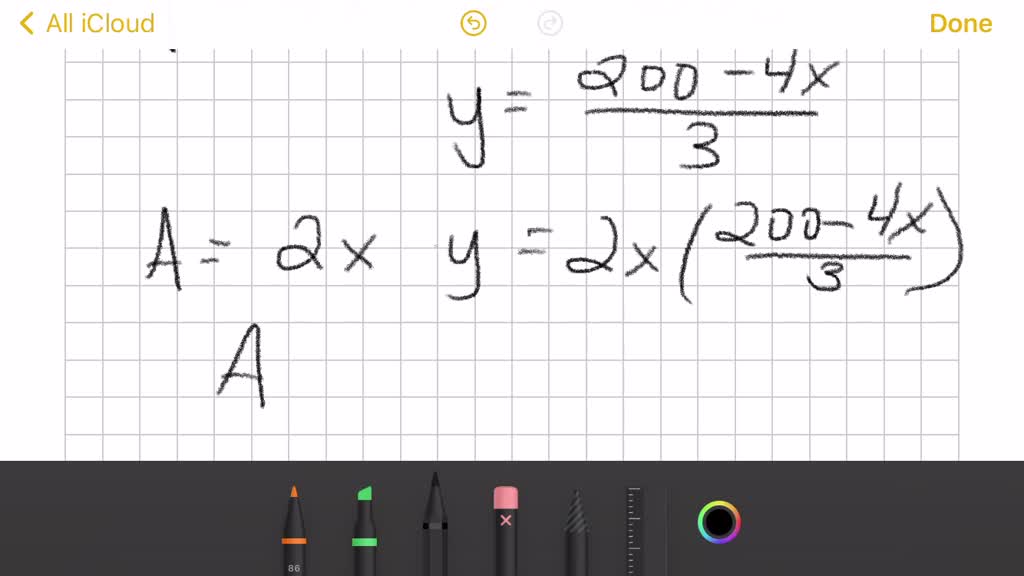Solved A Rancher Has 200 Feet Of Fencing To Enclose Two Adjacent Rectangular Corrals See Figure A Write The Area A Of The Corrals As A Function Of X B Create A
A rancher has 500 feet of fencing.
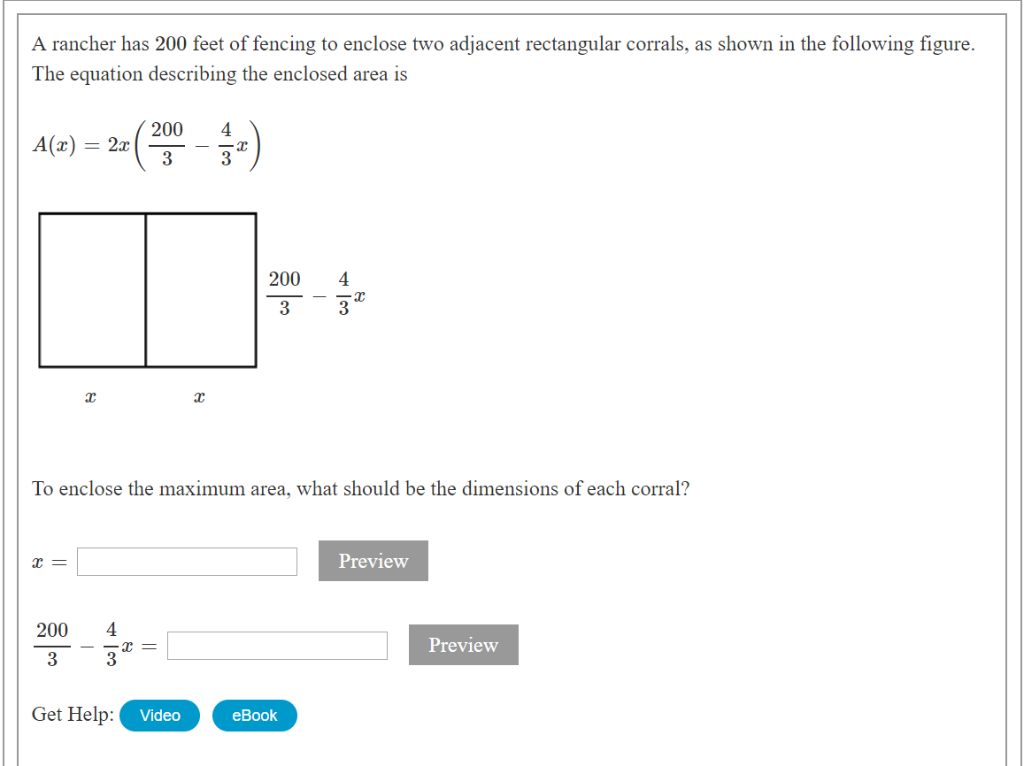
A rancher has 200 ft of fencing. Great -24 acre tract in the country. A rancher has 200 feet of fencing to enclose two adjacent rectangular corrals see figure. A rancher has 200 feet of fencing to enclose two adjacent rectangular corrals see figure.
B Create a table showing possible values of x and the corresponding areas of the corral. A rancher has 4 comma 7004700 feet of fencing available to enclose a rectangular area bordering a river. A rancher has 200 feet of fencing to enclose two adjacent rectangular corrals see figure.
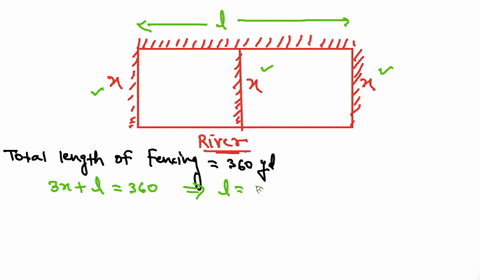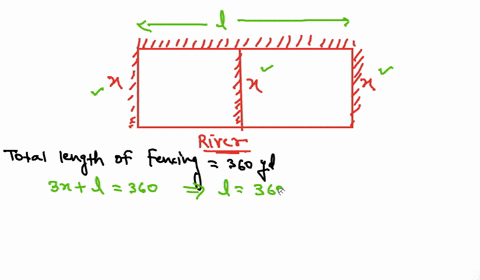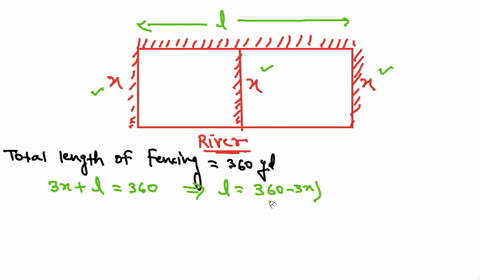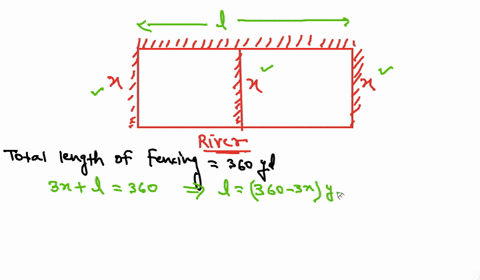
A rancher has 200 feet of fencing with which to enclose two adjacent rectangular corrals see figure. A rancher has 200 feet of fence with which to enclose three sides of a rectangular pasture the fourth side is a river and will not require fencing. Find the dimensions that maximize the enclosed area.
Let three corrals are in the form of square of Side x feet. If the fencing is 2 ft high what dimensions should the corral have in order to maximize its. The length with be the longer.
If no fencing is required along the river find the length. A rancher has 200 feet of fencing with which to enclose in two adjacent rectangular corrals. Find the dimensions of the.
A rancher has 600 feet of fencing to put around a rectangular field and then subdivide the field into 3 identical smaller rectangular plots by placing two fences parallel to one of the fields shorter sides. A rancher has 800 feet of fencing to put around a rectangular field and then subdivide the field into 3 identical smaller rectangular plots by placing two fences parallel to one of the fields shorter sides. Determine the dimensions of the corral that will maximize the enclosed area.
A rancher has 200 feet of fencing with which to enclose in two adjacent rectangular corrals. He wants to separate his cows and horses by dividing the enclosure into two equal areas. B create a table showing possible values of x and the corresponding areas of the corral.
B A spherical balloon is inflated with gas as the rate of 20 cube feet per minute. A rancher has 500 feet of fencing. A Write the area A of the corrals as a function of x.
If rancher wants to build a corral into three equal rectangles. A rancher has 200 feet of fencing to build a rectangular corral alongside an existing fence. A rancher has 1200 feet of fencing to enclose two adjacent rectangular corrals of equal lengths and widths as shown in the figure below.
A A rancher has 200 feet of fencing with which to enclose two adjacent rectangular corrals. Answer 1 of 8. Write your answers as.
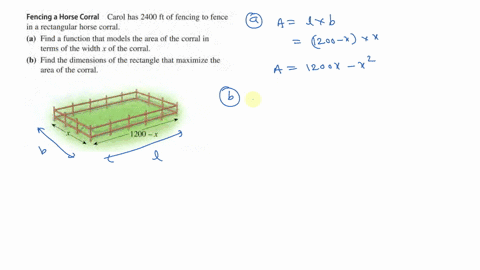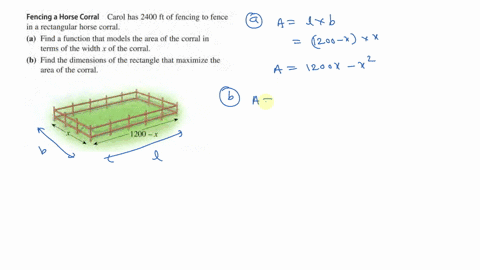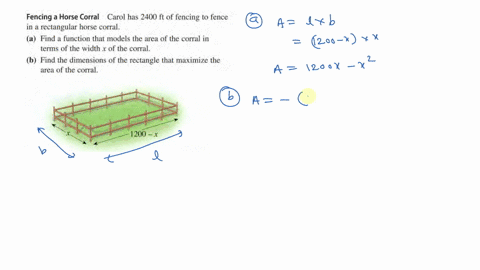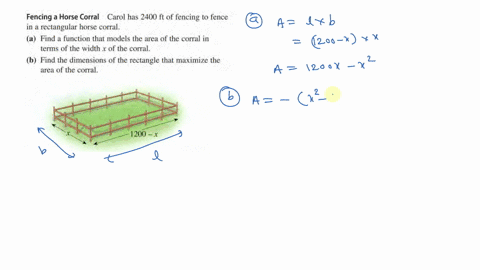
FIGURE CANNOT COPY a Write the area A of the corrals as a function of x. What dimensions should be used so that the enclosed area will be a maximum. What dimensions should be used so that the enclosed.
For the first rectangle and for the second. What dimensions should be used so that the enclosed area will be a maximum. Use complete-the-square to solve.
A rancher has 200 feet of fencing with which to enclose two adjacent rectangular corrals see figure. A rancher has 200 feet of fencing to enclose two adjacent rectangular corrals. What dimensions should be used so that the enclosed area will be a maximum.
In rectangular shape square will give the maximum area. Find the dimensions of the plot with the largest possible area. A rancher has 500 feet of fencing.
The Berniers have 24 ft of flexible fencing with which to build a rectangular toy corral. C use a graphing utility to graph the area function. What is the maximum area that can be enclosed in the fencing.
A rancher has 400 feet of fencing with which to enclose two adjacent rectangular corrals. What dimensions should be used so that the enclosed area will be a maximum. X y ft Need Help.
A rancher has 200 feet of fencing to enclose two adjacent rectangular corrals of the same dimensions. Use the table to estimate the dimensions that will produce the maximum enclosed area. What dimension should be used so that the enclosed area will be a maximum.
A write the area A of the corrals as a function of x. The figure is given as two adjacent rectangles side by side and the bottom is. A rancher has 200 ft of fencing to enclose two adjacent rectangular corrals.
Accordingly it has 6 Lengths and 4 Widths Perimeter 6x4x 400 Or 10x 400 Or x 40010. A rancher has 200 feet of fence with which to enclose three sides of a rectangular plot the fourth side is a cliff wall and will not require fencing.
Solved Maximum Area A Rancher Has 200 Feet Of Fencing To Enclose Two Adjacent Rectangular Corrals
Solved A Rancher Has 200 Feet Of Fencing To Enclose Two Adjacent Rectangular Corrals See Figure A Write The Area A Of The Corrals As A Function Of X B Create A
Solved A Rancher Has 200 Feet Of Fencing To Enclose Two Adjacent Rectangular Corrals See Figure A Write The Area A Of The Corrals As A Function Of X B Create A
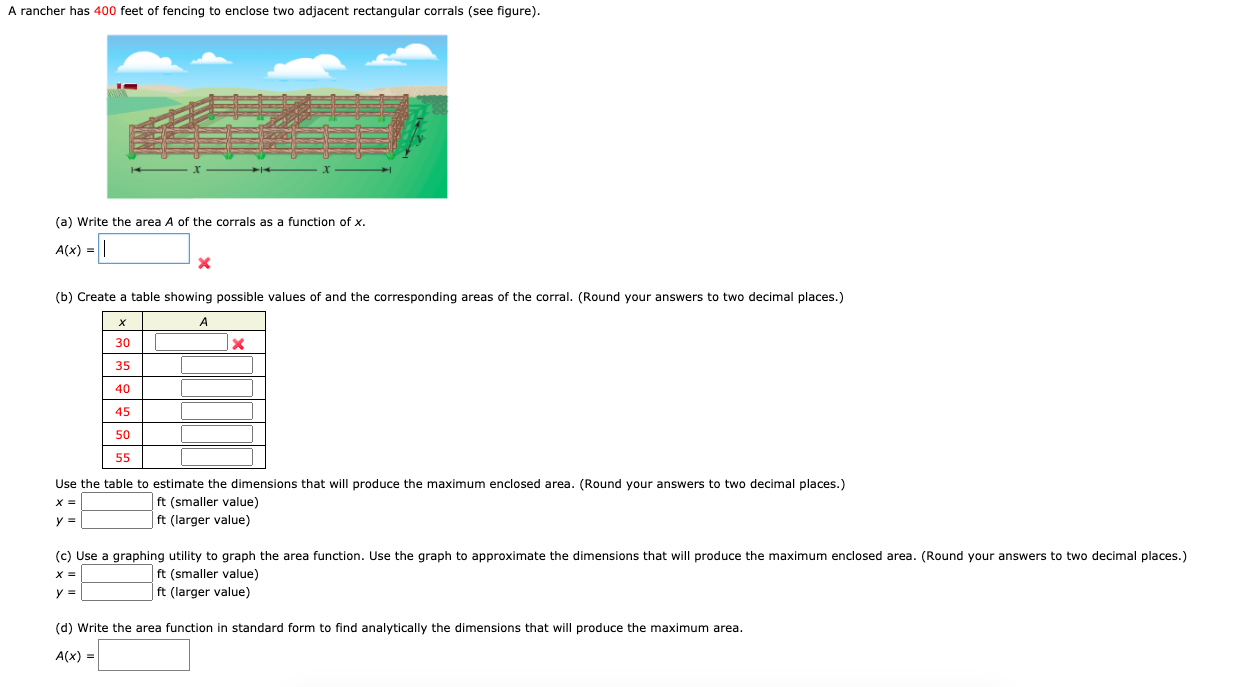Solved A Rancher Has 400 Feet Of Fencing To Enclose Two Chegg Com
Calculus Optimization Problems Fencing Problem Youtube
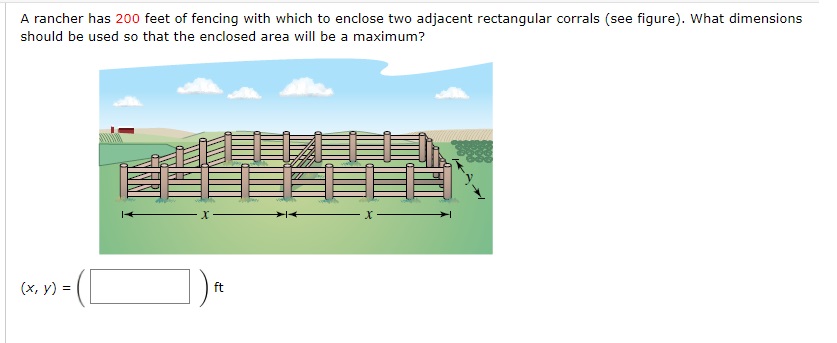
Solved A Rancher Has 200 Feet Of Fencing With Which To Chegg Com
Solved A Rancher Has 200 Feet Of Fencing With Which To Chegg Com
Answered A Rancher Has 200 Feet Of Fencing With Bartleby
A Rancher Has 200 Feet Of Fencing To Enclose Two Adjacent Rectangular Corrals What Dimension Should Be Used To So That The Enclosed Area Will Be A Enotes Com
Maximum Area A Rancher Has 200 Feet Of Fencing To Enclose Two Adjacent Rectangular Corrals What Dimensions Should Be Used So That The Enclosed Area Enotes Com
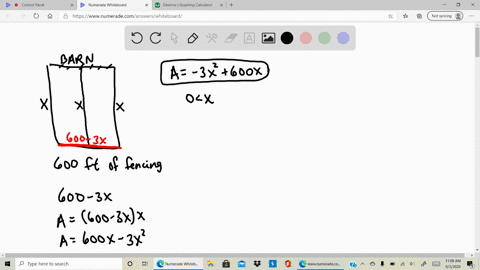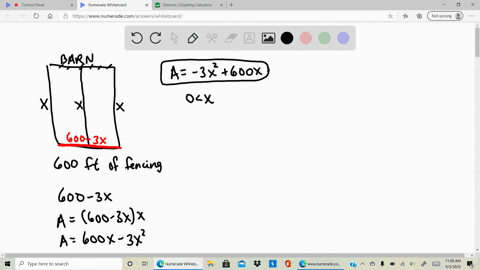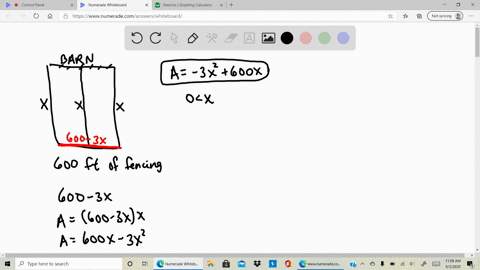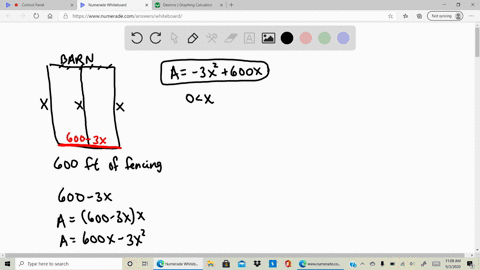Solved A Rancher Has 200 Feet Of Fencing To Enclose Two Adjacent Rectangular Corrals See Figure A Write The Area A Of The Corrals As A Function Of X B Create A
Optimization Problems 20 Youtube
Solved A Rancher Has 200 Feet Of Fencing To Enclose Two Adjacent Rectangular Corrals See Figure A Write The Area A Of The Corrals As A Function Of X B Create A
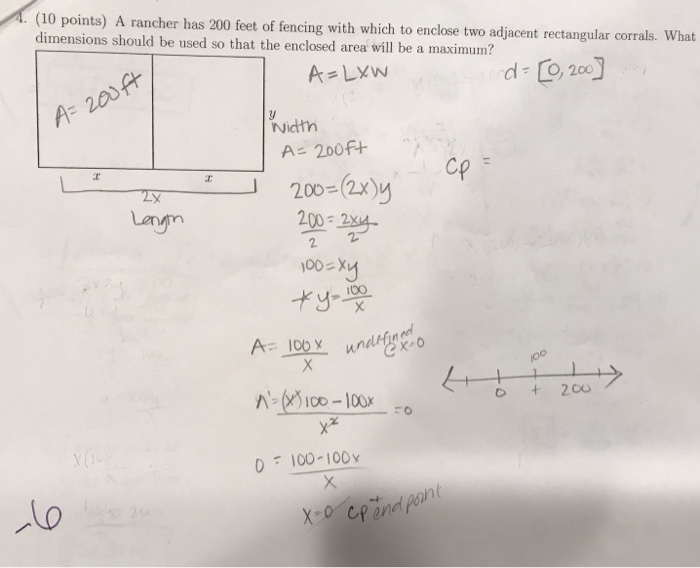
Solved A Rancher Has 200 Feet Of Fencing To Enclose Two Chegg Com
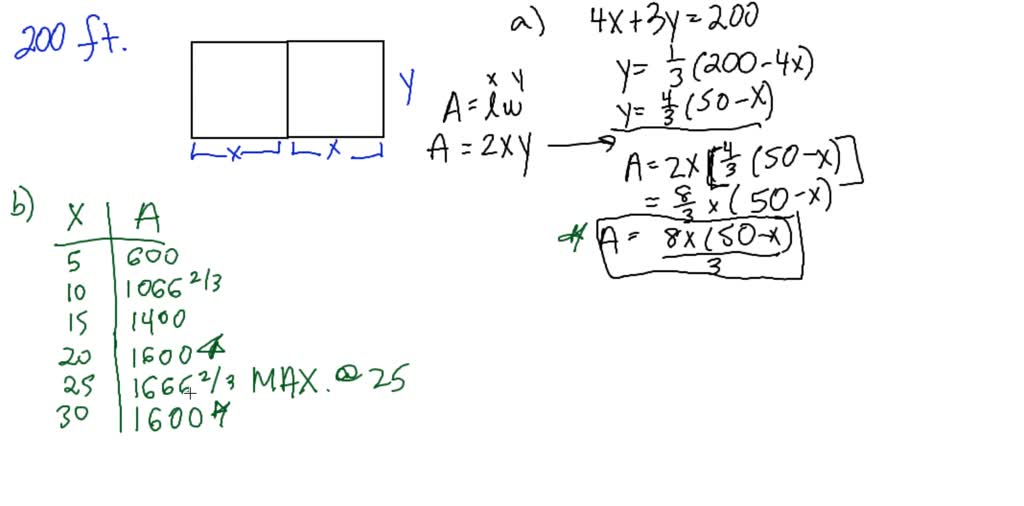Solved A Rancher Has 200 Feet Of Fencing To Enclose Two Adjacent Rectangular Corrals See Figure A Write The Area A Of The Corrals As A Function Of X
Solved A Rancher Has 200 Feet Of Fencing To Enclose Two Chegg Com
75 Numerical Graphical And Analytical Analysis By Paulina Cardenas
A Rancher Has 200 Feet Of Fencing To Enclose Two Adjacent Corrals A What Dimensions Should Be Used So Brainly Com
